Efficient Parallel Extraction of Crack-free Isosurfaces from Adaptive Mesh Refinement Data
Problem Statement and Goals
There are many forms of physical phenomena, like star formation, that occupy vast
regions of space. These areas have extreme variances in spatiotemporal scales, i.e.,
some areas are fairly homogeneous while other areas may change rapidly. To represent
these domains efficiently, simulations must vary the resolutions to adapt to local
features. The block-structured adaptive mesh refinement (AMR) approach addresses
this challenge by creating a hierarchy of axis-aligned rectilinear grids, which are
commonly referred to as
boxes. This representation requires less storage
overhead than unstructured grids—it is only necessary to store the layout of all
grids with respect to each other since connectivity within each rectilinear grid is
implicit—and makes it possible to represent different parts of the domain at
varying resolutions. Due to its effectiveness, an increasing number of application
domains use this simulation technique.
The hierarchical representation of AMR data makes data analysis particularly
challenging. It is necessary to take into account that a finer box may invalidate and
replace the value of a given grid cell. A greater challenge is in handling
transitions between hierarchy levels such that no discontinuities appear at the
boundaries between refinement levels. Like in many hierarchical data representations,
cracks in an extracted isosurface arise due to T-junctions between levels. These
cracks distract from a visualization's exploration- or communication-oriented
objective and introduce questions of correctness. Furthermore, they affect the
accuracy of quantities—such as surface area—derived from an isosurface.
Our goal was to design an algorithm for crack-free isosurface extraction that works
in a distributed-memory setting. We view the ability to run analysis on the system
that generates the data as a key requirement. Although some sufficiently high-memory
systems do exist to handle large data sets, the transfer time from the
distributed-memory supercomputer to this remote shared-memory system is generally
prohibitive.
Implementation and Results
Our new approach [1] extends from prior work using dual grids
and stitch cells to define continuous interpolation and isosurface extraction
simplifying its implementation by using a case table. The main design goals for
improving this approach were: (i) enabling data parallel stitch cell generation and
isosurface extraction that operate on individual AMR boxes separately, and (ii)
maintaining a rectilinear grid representation as long as possible.
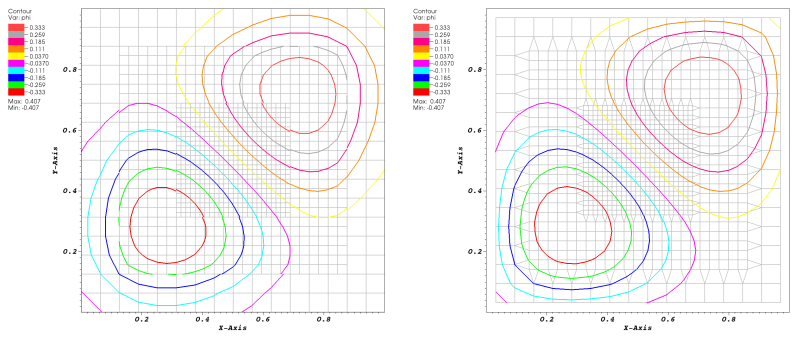
|
|
Figure 1: Extraction of crack-free isosurfaces from a 2D AMR data set. (Left)
Extracting contours using the standard marching cubes approach after re-sampling cell
centered AMR data to grid vertices (grid shown as light gray lines). The resulting
contours show clear discontinuities at the boundaries between levels.
(Right) Using original simulation data by using the dual grid connecting cell centers
and filling resulting gaps between levels with procedurally generated stitch cells
yields contours continuous at level boundaries.
|
Like in the previous approach, we use dual grids---connecting the cell centered
values produced by the simulation---and stitch cells filling the gaps between those
dual grids---see Figure 1. Stitch cells correspond to linear VTK
cells (hexahedron, pyramid, wedge and tetrahedron) with values specified at the
defining vertices. Our work uses a single case table to create stitch cells, which
improves the original approach by making it easier to implement and maintain in
visualization software.
Stitch cells connect a box to its neighboring boxes in the same level, or
containing/adjacent boxes in the coarser parent level. To construct stitch cells and
assign values to their vertices, we require access to adjacent samples in these
boxes. To facilitate parallelization, we utilize
ghost cells, a concept
originating from simulation. By extending grids with a one-cell wide layer of cells
and filling these cells with values from adjacent grids or the next coarser level,
all data required to construct stitch cells are available locally, and it becomes
possible to process AMR data on a per-box basis.
In simulations, ghost data is normally used at the boundaries to support, e.g., the
computation of gradients using only data locally available. For visualization
purposes, these cells are typically blanked out, or any generated geometry
corresponding to them is removed. It is possible to use a similar concept to handle
cells in a box that are invalidated by a finer resolution box. Instead of removing
individual cells from a box, by either converting boxes to unstructured meshes or a set
of boxes that leaves out refined regions, it is more computationally and storage
efficient to keep values in these cells and mark them as “ghost.” This gives rise to
a new type of “ghost cell,” i.e., one ghost cell marked as invalid because there is a
more accurate data representation available. We handle ghost data at the boundaries
as well as ghost data due to invalidation by finer grids, by using an array of flags
that specify for each grid cell whether it is a ghost cell or not. If a cell is
flagged as ghost, the flag also specifies its type. All visualization algorithms
operate on the original rectilinear grids and use the ghost array information to
blank out ghost cells. This is the standard implementation in VisIt. In the dual
grid, a cell is marked as ghost if any of the cells in the original grid
corresponding to its vertices is labeled as a ghost cell, i.e., if it connects any
samples that are flagged as invalid.
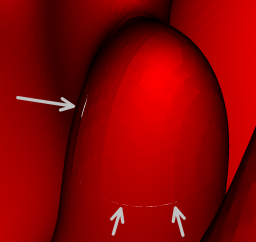


|
|
Figure 2: Isosurface (temperature of 1225K) for the hydrogen flame data set. (i)
Close-up view of the isosurface extracted via re-sampling to a vertex-centered
format. Cracks are easily visible. (ii) Close-up view of the same region extracted
using our new method. There are no discontinuities in the isosurface. (iii) View of
the entire crack-free isosurface extracted using our new approach. The isosurface
consists of approximately 2.2 million triangles.
|
To test our algorithm we examined results from two data sets on the Hopper system
at the National Energy Research Scientific Computing Center (NERSC). The first data
set is a relatively small 3D BoxLib AMR simulation of a hydrogen flame. It consists
of 2,581 boxes in three hierarchy levels containing a total of 48,531,968 grid cells.
The simulation data size for all 22 scalar variables is 8.1GB, which is approximately
377MB per scalar variable. Figure 2 highlights the
difference between an isosurface extracted from a re-sampled data set and the
continuous isosurface provided by our new approach. We stored this data set on the
local scratch file system.
The second data set is a larger 3D BoxLib AMR simulation of a methane flame. This
data set consists of 7,747 boxes in 3 levels containing a total of 1,525,420,032 grid
cells. The data set has a total size of 592GB for 52 scalar variables, which
corresponds to a size of approximately 11.4GB per scalar variable. We stored this
data set on the global NERSC file system. Both data sets were provided by the Center
for Computational Sciences and Engineering (CCSE) at the Lawrence Berkeley National
Laboratory (LBNL).
In these experiments, we saw excellent scaling of the stitch cell algorithm, as well
as of the following contouring operation, even on the small data set. Unfortunately,
we reached the best overall performance with this visualization pipeline at only 120
cores. Although disk I/O is one factor limiting the scaling in this example, the main
bottleneck is the ghost data generation phase, as we see its runtime increase with
core count. Using a simple model that assumes two fixed transfer rates for intra- and
inter-node communication time, we found that the increased amount of ghost data
duplicated in the distributed-memory setting explains the increase in ghost
communication time. We also examined performance of this same visualization pipeline
on the larger methane flame data set. The results showed a significantly better scaling
performance for total runtime on this larger data set than on the smaller hydrogen
flame data set.
Impact
Our approach extracts crack-free isosurfaces in a distributed-memory setting
encountered on many DOE high-performance computing platforms. It is deployed as part
of the VisIt visualization tool, which makes it easily available on these platforms. AMR
is used for a wide range of DOE relevant application domains (fusion, astrophysics,
climate, carbon sequestration), and the ability to extract “correct” isosurfaces
benefits data analysis in all these areas. Furthermore, our dual grid and
stitch-cell based approach can be used to improve other visualization algorithms
(e.g., volume rendering) as well. Finally, this approach could form the basis for
deriving topological structures like the contour tree from AMR data.
References
[1]
Gunther H. Weber, Hank Childs, and Jeremy S. Meredith.
Efficient Parallel Extraction of Crack- free Isosurfaces from Adaptive Mesh Refinement (AMR) Data.
In Proceedings of IEEE Symposium on Large Data Analysis and Visualization (LDAV), pages 31-38, October 2012.
LBNL-5799E.
Contact
Gunther H. Weber,
Hank Childs.
Collaborators
Jeremy Meredith